今回はギターの固有振動数の測定方法についてお話したいと思います。

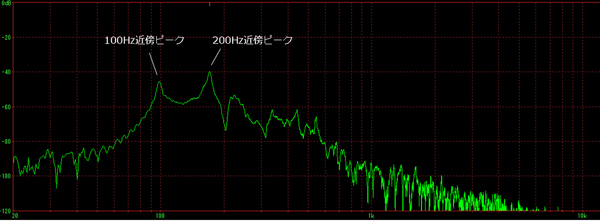
Fig.2-1は、あるギターの共振特性を測定したものです。横軸は周波数、縦軸は周波数毎の応答の強さを表しています。また、100Hz近傍と200Hz近傍にピークが２つありますが、この周波数が固有振動数です。瓢箪形状をしていれば、どのメーカーのギターも、この傾向はほぼ同じようです。といってもすべてのメーカーを測定したわけではありませんが。

　　　　　　　　　　     Fig.2-1

さて、この共振特性をどうやって測定するか、についてですが、
横軸が周波数で、縦軸がその応答であるなら、周波数が順に変化するスイープジェネレータをスピーカーにつないで音を出し、その音をギターボディーに当てて、その時の振動を測定すればいい、ということになります。でも、これって、実際にやるとなると結構大変なことです。

そこで、より簡易的な測定法として知られているものが、インパルス応答を利用した測定法です。Fig.2-2に示すような信号処理系があったとします。

入力信号xを特性hの線形システムに入力した時、出力がｙとなるようなシステムです。時間領域においては、出力yは、入力xと特性hの畳込み積分によって表すことができます。x,h,yのフーリエ変換をそれぞれ X,H,Yとすれば、周波数領域では、出力YはHとXの単純な積で表すことができます。ここで、システムをギターそのもの、入力を外部から与えられる振動（弦を弾いた時の振動）と考えれば、与えられた入力に対して出力Y、すなわちギターがどのように振る舞うかを把握することができます。

次に、インパルスが入力された場合を考えます。インパルスとはパルス幅がゼロ、パルス高が無限大である仮想的な信号のことであり、そのフーリエ変換 X = F(x) = 1 となります。つまり、インパルスは、直流から無限大に至るまでの全周波数を含んでいる信号なのです。このインパルスをFig.2-2に入力すると、

　　X = F(x) = 1

ですから、周波数領域の出力は

　　Y = H・X = F(h)・F(x) = F(h)・1 = F(h)

となり、システムの特性F(h)がそのまま出力として現れることになります。
つまり、ギターにインパルスを与えると、ギターのボディーの特性そのものを測定できることになります。前述のとおり、インパルス自体は仮想的な信号ですが、これをいわゆるタッピング（指などでボディーをたたいて音を出す）で代用することによって、近似的にインパルス応答（Fig.2-2に示すような波形）を得ることができます。

以上、簡単に言いますと、ギターのボディーをタッピングして発生する音をマイクで収音し、フーリエ変換すると、Fig.2-2に示すような周波数特性を近似的、簡易的に測定することができる、ということになります。

蛇足ですが、タッピングは上記の他に
　・接着の確認
　・Top/Backの厚さ分布の調整
　・ブレーシング調整、全体的な音のバランス
等で使われており、ギターを制作する上ではとても重要な技術といえます。
この辺の詳細については、また別の機会にでも。

 

ギターの固有振動（１）に戻る　　　　　ギターの固有振動（３）に進む