ギターに限らず、あらゆる物体には　「固有振動数　＝　一番振動しやすい振動数」　というものがあります。固有振動数は１つとは限らず、物体によっては複数存在する場合もあります。 東日本大震災の際に、新宿の高層ビルがゆらゆら揺れている映像がTVで報道されていましたが、あれは、地震波の振動数がビルの固有振動数に近いものであったため、ビルに固有振動が生じたものです。

では、ギターの弦の振動が、ギターボディーの固有振動数に一致したらどうなるでしょうか？　

少なくとも、本来出したい音とは違った音になることは容易に推測できます。そのため、ギターの固有振動数を把握し、その影響を低減することは、ギターを制作する上でとても重要になってきます。そこで、これより何回かに分けて、ギターの固有振動についての話を書いてみたいと思います。ちなみに、固有振動を共振と読み替えて戴いても結構です。

まず今回は前置き的な話となりますが、「ヘルムホルツ共振」についてです。

ビール瓶の口に、横からフーッと息を吹きかけると、「ボーッ」と音がでますが、あれが、ヘルムホルツ共振と言われるものです。Fig.1-1に示すように、フーッと息を吹きかけることによって、瓶の口の上部の気圧が下がり、瓶内部の空気が外へ出ようとします。しかし、瓶内部では外へ出る空気を戻そうとする力が働きますので、瓶の内部と外部で綱引き状態となります。その結果、空気が上へ行ったり、下へ行ったりを繰り返す、つまり、空気が振動するという現象がおきます。音はすなわち空気の振動ですので、この時の振動数に相当する「ボーッ」という音が出るわけです。

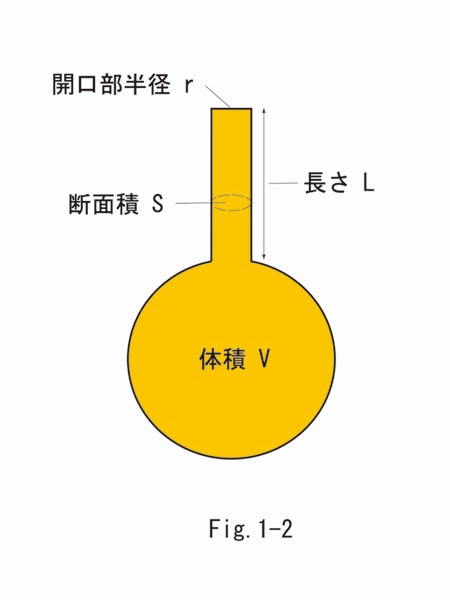
Fig.1-2に示す、球体の体積がV、ネックの断面積がS、ネックの長さがL、開口部半径ｒのフラスコの場合、ヘルムホルツ共振の振動数はFig.1-3に示す式によって計算されます。フラスコの球体をギターのボディー（共鳴胴）、サウンドホールをフラスコのネックと考えると、ギターでもヘルムホルツ共振が起こることが容易に推測できます。また、Fig.1-3で示した式は、空気の振動がフラスコ内部のみで起こるという理想的なケースですが、実際はフラスコの上部まで空気が振動するため、ネック長は実測値Lではなく有効長L’という値が用いられます。ギターの場合には、一般的に L’ = L + 1.7r という値になることが知られています。といっても、Fig.1-3の式にはSIDE板が固定されて振動しない場合などの条件がありますが、実際はそうではありませんし、サウンドホール形状やTOP板の厚さや材質、SIDE板の厚さ、材質等によっても変わってきますので、あくまで大まかに現象を定性的に捉えるための式と考えた方が良さそうです。

さて、Fig.1-3の式を見るとわかるように、ネック断面積Sが小さくなったり、あるいは、球体の体積Vが大きくなったり、ネック長L’　が長くなったりすると、固有振動数fは小さくなることがわかります。つまり、ギターで言えば、サウンドホール径が小さくなったり、ボディーが大きくなったりすると固有振動数fは低い方へ移動していくことになります。

少し話は脱線しますが、、、
この原理を応用して、ギターのサウンドホールにトルナボスという共鳴胴を取り付けて低音を強調したりすることも行われています。つまり、フラスコのネック部分を長くすることによって、固有振動数を低い方へ動かして低音強調する訳です。サウンドホールの直径はだいたい100mmくらいですが、カップ麺の容器の直径も100mmくらいですので、Fig.1-4のように、これをはさみでちょん切ってトルナボスを製作して、ちょっと音を聞いてみるくらいの実験は簡単にできますので、興味のある方は試してみてください。
音はどう変化するでしょうか？　
確かに低音は協調されたように感じます。ですが、音の輪郭も失われるように感じますので、個人的にはあまり好きな音とは言えません。

ということで、今回はギターはヘルムホルツ共振と深い関係があるというお話でした。

続きはまた次回。

 

ギターの固有振動（１）に戻る　　　　　ギターの固有振動（２）に進む